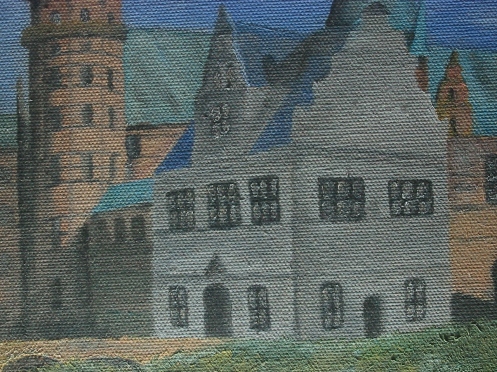Enhancement in the Frequency Domain

The activity is primarily concerned with improving an image’s quality by filtering unwanted elements in Fourier space. We will tackle this in two parts: familiarizing ourselves with the Fourier Transform of multiple elements (through convolution theorem) and finally applying it to actual images.

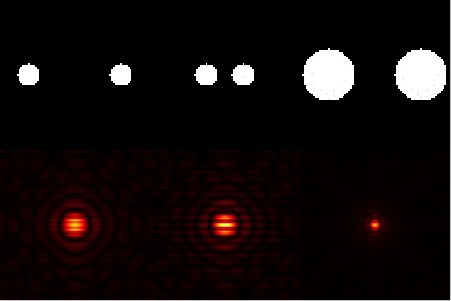
Before we start with convolution, first we need to familiarize ourselves with the Fourier Transforms of common shapes. Below is a table of figures that show some common figures and their Fourier transforms. Radially symmetric Dirac deltas produce a sinusoid along their common axis, a circle will create an Airy disc, and a square will result in a sinc function in both x and y axes. It should also e noted that a wider image will be further reduced in Fourier space. This is why a gaussian with high variance will appear small in Fourier  space.

Now that we know this, we can make use of the convolution theorem.The convolution theorem says that the Fourier Transform of a convolution between two functions is the same as the product of the Fourier Transform of those two functions. Take for example the images below and their Fourier Transforms.

The two circles in the image can be taken as the convolution between two radially symmetric Dirac deltas and a circle. Applying the convolution theorem, the Fourier Transform of the image should be the product of a sinusoid and an Airy disk, which we observe in the image above, where the sinusoid and the Airy disk are combined into one image. Decreasing the distance between the two Dirac deltas would change the frequency of the resulting sinusoid in Fourier space, and this remains true when applying the convolution theorem. The same is true for the inverse proportionality of sizes between real space and Fourier space.

Below are a few more examples of a Dirac delta convolution with squares and gaussians:

Using the convolution theorem, we can easily make a convolution of two individual images. Following the theorem, one would simply need to take the inverse Fourier Transform of the product of the Fourier Transform of the individual images. We demonstrate this by creating an image with random points and an image of a 5×5 pattern in the center.

We take the individual Fourier Transforms of the images as shown below.

Multiplying the two images together point by point and taking the inverse Fourier Transform, we achieve the final result,

The convolution looks as if the 5×5 pattern was smeared onto each of the random points  in the original image.

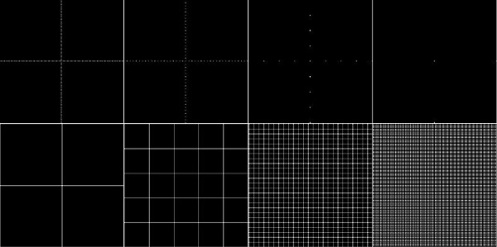
We also observe the Fourier Transform of equally spaced points along the x and y axis. Shown below are the patterns in increasing distances between points and their corresponding Fourier Transforms.

As we can observe from the image, the number of lines appearing in Fourier space increases in proportion with the distances between the points. The first column, where the points are separated only by one pixel, have produced only one line per axis. On the other hand, the last column, where the pixels are separated by 99 pixels, produce so many lines that it is a serious chore to count them manually.

Now that we are comfortable with the convolution theorem, we can move on to improving image quality by manipulation in the Fourier space. If a certain artifact is present in an image, and this artifact has some form of pattern throughout the image, this pattern will manifest itself as certain points in Fourier space. By filtering these points, we can remove them from the original image.

Our first example is the picture of the Lunar Orbiter image. Present in the picture are horizontal lines, which are the result of combining different frames. Since the artifact we are observing is limited only to being repeated along the y-axis, we can already predict that the points we will be filtering are present on the y-axis.

Above to the left is the Fourier Transform of the image. The central mask is there in order to make the other artifacts more visible. As expected, we observe equally spaced points along the y-axis. We take note of their coordinates and zero them, as shown in the image to the right.

With the unwanted frequencies removed, it is a simple matter of performing an inverse Fourier Transform. The resulting image has greatly improved compared to the original, though there are still minor traces of the horizontal lines.

We try again on another image, a picture of a painting on woven fabric. Our goal this time is to remove the artifact caused by the weaving on the fabric surface.

Observing the weaving pattern, we note that repetition can be seen in multiple directions. Unlike the previous image, where the artifacts were limited to the y-axis, we expect our points of interest to be scattered about the Fourier space. We take the grayscale of the image so that we are only working with a 2D matrix of values and use a Fourier Transform.

The above image is the Fourier Transform with the center masked. We are able to observe distinct points surrounding the center, and it is these points we will be filtering. Once filtered, we take the inverse Fourier Transform to obtain,

 

The image above is the frequency filtered image. As we can see, the processed image, though still retaining minimal details of the weaving, has been greatly improved as compared to the original.

Since the processing isolated the weaving pattern, it is also possible to reconstruct it. Inverting the mask used on the image and performing an inverse Fourier Transform, the results is:

The image above is a magnified center of the inverse Fourier Transform of the mask. As we can see, it does resemble the weaving pattern on the original image.

It is worth noting that one need not restrict himself to grayscale images when filtering frequencies. Given a truecolor image, simply separate the red, green, and blue channels and process them separately. Unless the artifact is something restricted to one channel, the same mask can apply for all channels, and even if this is the case, using the same mask should not affect the quality greatly. Below is a processed color image with each channel processed using the same mask.

For this activity, I will be giving myself a 12/10 since I was able achieve the desired results and was able to explore filtering color images.